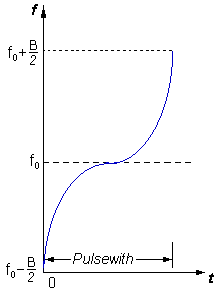
Pulse Compression
|
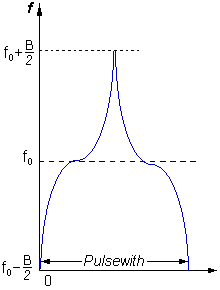
Since each part of the pulse has unique frequency,
the returns can be completely separated. This modulation or coding can be either
|
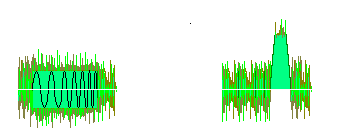  Figure 1: separation of frequency modulated pulses |
Now the receiver is able to separate targets with overlapping of noise. The received echo is processed in the receiver by the compression filter. The compression filter readjusts the relative phases of the frequency components so that a narrow or compressed pulse is again produced. The radar therefore obtains a better maximum range than it is expected because of the conventional radar equation.
The ability of the receiver to improve the range resolution over that of the conventional system is called the pulse compression ratio (PCR). For example a pulse compression ratio of 50:1 means that the system range resolution is reduced by 1/50 of the conventional system.
Alternatively, the factor of improvement is given the symbol PCR, which can be used as a number in the range resolution formula, which now becomes:
The compression ratio is equal to the number of sub pulses in the waveform, i.e., the number of elements in the code. The range resolution is therefore proportional to the time duration of one element of the code. The maximum range is increased by the PCR.
The minimum range is not improved by the process. The full pulse width still applies to the transmission, which requires the duplexer to remained aligned to the transmitter throughout the pulse. Therefore Rmin is unaffected.
| Advantages | Disadvantages |
|
lower pulse-power therefore suitable for Solid-State-amplifier |
high wiring effort |
| higher maximum range | bad minimum range |
| good range resolution | time-sidelobes |
| better jamming immunity | |
| difficulties reconnaissance |
Pulse compression with linear FM waveform
At this pulse compression method the transmitting pulse has a linear FM waveform. This has the advantage that the wiring still can relatively be kept simple. However, the linear frequency modulation has the disadvantage that jamming signals can be produced relatively easily by so-called „Sweeper”.
The block diagram on the picture illustrates, in more detail, the principles of a pulse compression filter.
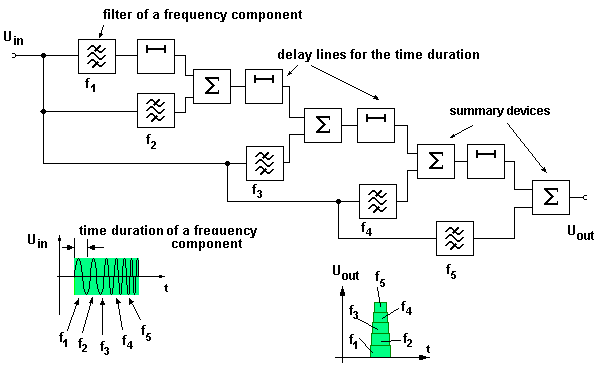
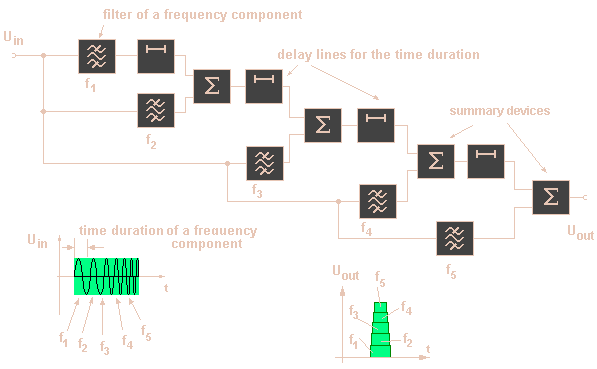
Figure 1: Block diagram
The compression filter are simply dispersive delay lines with a delay, which is a linear function of the frequency. The compression filter allows the end of the pulse to „catch up” to the beginning, and produces a narrower output pulse with a higher amplitude.
As an example of an application
of the pulse compression with linear FM waveform the
Filters for linear FM pulse compression radars are now based on two main types.
- Digital processing (after an A/D- conversion).
- Surface acoustic wave devices.
Time-Side-LobesThe output of the compression filter consists of the compressed pulse accompanied by responses at other times (i.e., at other ranges), called time or range sidelobes. The figure shows a view of the compressed pulse of a chirp radar at an oscilloscope and at a ppi-scope sector. Amplitude weighting of the output signals may be used to reduce the time sidelobes to an acceptable level. Weighting on reception only results a filter „mismatch” and some loss of signal to noise ratio. The sidelobe levels are an important parameter when specifying a pulse compression radar. The application of weighting functions can reduce time sidelobes to the order of 30 db's. |
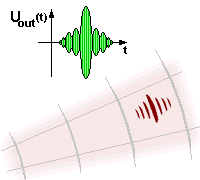 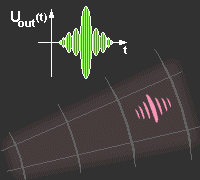 Figure 2: View of the Time-Side-Lobes |
Pulse compression with non-linear FM waveform
The non-linear FM waveform has several distinct advantages. The non-linear FM waveform requires no amplitude weighting for time-sidelobe suppression since the FM modulation of the waveform is designed to provide the desired amplitude spectrum, i.e., low sidelobe levels of the compressed pulse can be achieved without using amplitude weighting.
|
Matched-filter reception and low sidelobes become
compatible in this design. Thus the loss in
signal-to-noise ratio associated with weighting by
the usual mismatching techniques is eliminated. A symmetrical waveform has a frequency that increases (or decreases) with time during the first half of the pulse and decreases (or increases) during the last half of the pulse. A non symmetrical waveform is obtained by using one half of a symmetrical waveform. The disadvantages of the non-linear FM waveform are
|
Picture 1: symmetrically waveform
Picture 2: non-symetrically waveform 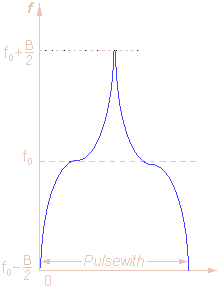
Picture 1: symetrically waveform 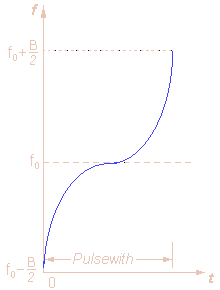
Picture 2: non-symetrically waveform |
Phase-Coded Pulse Compression
Phase-coded waveforms differ from FM waveforms in that the long pulse is sub-divided into a number of shorter sub pulses. Generally, each sub pulse corresponds with a range bin. The sub pulses are of equal time duration; each is transmitted with a particular phase. The phase of each sub-pulse is selected in accordance with a phase code. The most widely used type of phase coding is binary coding.
| The binary code consists of a sequence of either +1 and -1. The phase of the transmitted signal alternates between 0 and 180° in accordance with the sequence of elements, in the phase code, as shown on the picture. Since the transmitted frequency is usually not a multiple of the reciprocal of the sub pulsewidth, the coded signal is generally discontinuous at the phase-reversal points. |
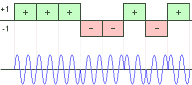 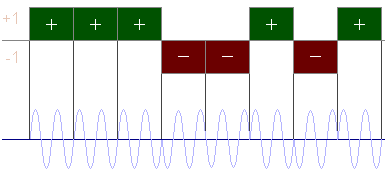 Picture 1: diagram of a phase-coded pulse compression |
|
The selection of the so called random 0, π phases is
in fact critical. A special class of binary codes is
the optimum, or Barker, codes. They are optimum in
the sense that they provide low sidelobes, which are
all of equal magnitude. Only a small number of these
optimum codes exist. They are shown on the beside
table. A computer based study searched for Barker
codes up to 6000, and obtained only 13 as the
maximum value.
It will be noted that there are none greater than 13 which implies a maximum compression ratio of 13, which is rather low. The sidelobe level is -22.3 db. |
|
|||||||||||||||||||||||||||||||
|
Table: Barker Codes |